首页->综合电路图
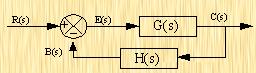 fanxiaoxi 2024-09-13
fanxiaoxi 2024-09-13
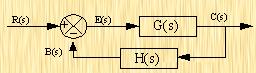 fanxiaoxi 2024-09-13
fanxiaoxi 2024-09-13
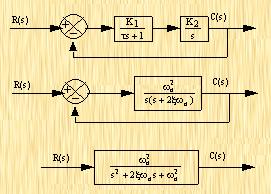 fanxiaoxi 2024-09-13
fanxiaoxi 2024-09-13
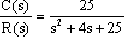 fanxiaoxi 2024-09-13
fanxiaoxi 2024-09-13
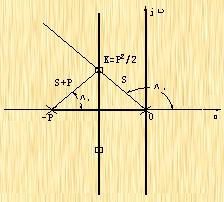 fanxiaoxi 2024-09-13
fanxiaoxi 2024-09-13
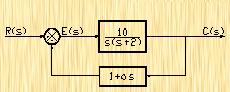 fanxiaoxi 2024-09-13
fanxiaoxi 2024-09-13