自适应滤波器的作用、原理以及相关应用
自适应滤波器是指根据环境的改变,使用自适应算法来改变滤波器的参数和结构的滤波器。一般情况下,不改变自适应滤波器的结构。而自适应滤波器的系数是由自适应算法更新的时变系数。即其系数自动连续地适应于给定信号,以获得期望响应。自适应滤波器的最重要的特征就在于它能够在未知环境中有效工作,并能够跟踪输入信号的时变特征。
自适应滤波器的作用
1、系统辨识:这时参考信号就是未知系统的输出,当误差最小时,此时自适应滤波器就与未知系统具有相近的特性,自适应滤波器用来提供一个在某种意义上能够最好拟合未知装置的线性模型。当我们想描述一个未知系统(如一组复杂的模拟电路),解析的算出系统的冲击响应或者系统函数是比较困难的。这时,我们就可以用未知系统的输入和输出训练自适应滤波器(未知系统的输入作为自适应滤波器的输入,未知系统的输出作为自适应滤波器的期望信号,当自适应滤波器收敛后,对应的滤波器就可以看做是未知系统的近似)。
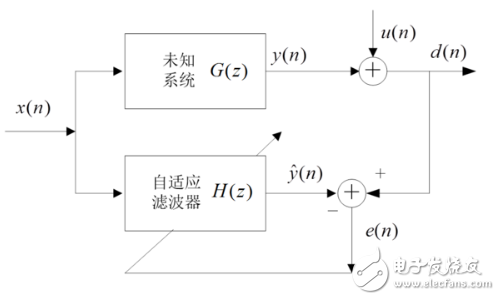
2、逆系统辨识:在这类应用中,自适应滤波器的作用是提供一个逆模型,该模型可在某种意义上最好拟合未知噪声装置。理想地,在线性系统的情况下,该逆模型具有等于未知装置转移函数倒数的转移函数,使得二者的组合构成一个理想的传输媒介。该系统输入的延迟构成自适应滤波器的期望响应。在某些应用中,该系统输入不加延迟地用做期望响应。
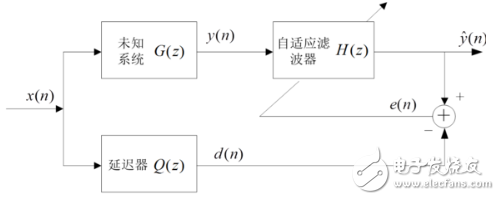
3、预测:在这类应用中,自适应滤波器的作用是对随机信号的当前值提供某种意义上的一个最好预测。于是,信号的当前值用作自适应滤波器的期望响应。信号的过去值加到滤波器的输入端。取决于感兴趣的应用,自适应滤波器的输出或估计误差均可作为系统的输出。在第一种情况下,系统作为一个预测器;而在后一种情况下,系统作为预测误差滤波器。
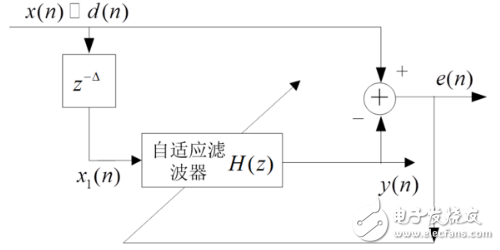
4、干扰消除:在一类应用中,自适应滤波器以某种意义上的最优化方式消除包含在基本信号中的未知干扰。基本信号用作自适应滤波器的期望响应,参考信号用作滤波器的输入。参考信号来自定位的某一传感器或一组传感器,并以承载新息的信号是微弱的或基本不可预测的方式,供给基本信号上。这种类型自适应滤波器的输入信号为噪声源,期望信号信号为含有噪声的信号源。经过多次迭代后,期望信号和自适应滤波器的输出信号之差就是信号源的估计。
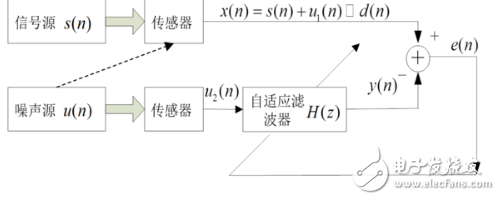
自适应滤波器的原理
1、最小均方(LMS)误差算法:
最简单的LMS算法是通过每一次迭代输入的数据对当前的目标函数的梯度进行估计,从而得到相应输入信号的自相关矩阵R与互相关向量p。则得到的梯度估计值为:
gw(k)=-2p(k)+2R(k)w(k)=2x(k)(-d(k)+w(k)(k))=-2e(k)x(k)
则滤波系数更新方程为:w(k+1)=w(k)+2niu*e(k)x(k)
整理可得LMS算法:
初始化部分:
w(k)=[00…0]T
单次迭代部分:
e(k)=d(k)-w(k)(k)
w(k+1)=w(k)+2niu*e(k)x(k)
其中niu参数表示单次调节的步长,是一个常数需要在实际的应用中进行确定。我们可以得到单次迭代所需要进行的乘法次数为O[N]量级,N表示FIR滤波器的系数矢量w(k)的维数,该算法已经具有一定的实际应用的价值,如果对滤波的精度要求不是很高,而且对每次迭代速度有很高的要求的话,此算法非常合适。
2、递归最小二乘(RLS)算法:
在上一节中我们知道,基于瞬时梯度估计的LMS算法实际上只使用了当前时刻的输入信号矢量x(k)和期望信号d(k),没有利用过去的信息这就导致梯度估计的误差很大算法收敛的数度慢,一个很直接的想法就是如果能把过去的信息利用起来,那么梯度估计的误差就会大大的减小,算法很快就会收敛。最小二乘(RL)算法正好就实现了这一过程,它旨在使期望信号与模型滤波器输出之差的平方和最小。具体的算法推导比较的复杂,这里不方便编辑公式同时也没有必要,在这里给出了其算法实现语言描述部分。

下面对其中的一些相关变量名做一下解释,SD(k)表示输入信号矢量的确定性自相关矩阵(RD(k))的逆,e(k)表示先验误差,epsilon(k)表示后验误差(就是图片中的希腊字母epsilon,由于不方便输入所以用它代替了,后面还有一个哦),lambda表示遗忘因子,意思就是随着时间的推移以前的“旧”的信号对滤波器系数调整的影响越小,主要由更新的数据决定,从这个角度说明了该算法对非平稳的信号也能进行自适应滤波。其它的变量同上。从上面的描述可以看出单次迭代运算量在O[N2]量级,比LMS的计算量要大。



评论