正反馈回路和非最小相位系统根轨迹

正反馈回路和非最小相位系统根轨迹

4.7.1 正反馈回路根轨迹 ⒈引言： 前面介绍的绘制根迹的依据、法则，都是针对负反馈系统的。对于正反馈，前面的依据、规则，需要作些修改，修改以后的规则，可被用来画正反馈回路的根迹。 ⒉修改内容： ⑴.作图依据： ①.特征方程： ②.幅角条件：故称零度根轨迹。 ③.幅值条件：和前面一样。 ⑵.作图规则： ①.实轴上根迹：为所在线段的右面有偶数个开环零、极点。 ②.(n-m)条渐近线倾角： k=0,1,2 ③.根迹的出射角、入射角： ⒊结论： 按零度根轨迹规则，绘制正反馈回路根轨迹，其步骤同负反馈。下面举例说明。 例4-6 设一反馈系统内回路为正反馈，如图4-20所示，其开环传递函数为：

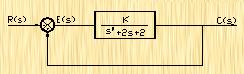图4-20

试绘制其内回路根轨迹。

图4-20

⑴.常规方法

①.两条根迹分支：分别起始于两个开环极点-1+j, -1-j，终止于s平面∞处。

②.实轴上根迹：因为实轴无开环零、极点，所以整条实轴是根迹。

③.两条渐近线之倾角: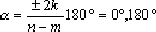

④.开环极点-1+j的出射角: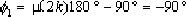

⑤.会合点：由公式

⑥.复平面上的根迹: 由幅角条件可知，两个开环极点之间的连线是根迹。

⑦.所求根迹，如图4-21所示。

⑵. “MATLAB”方法

解本题的MATLAB程序exe46.m：

n=[-1];
d=[1 2 2];
rlocus(n,d)
title(‘4-21’)

执行本程序,可得正反馈根轨迹图4-21

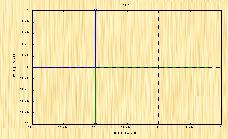图4-21

4.7.2 非最小相位系统之根迹

所谓非最小相位系统:

如果系统的所有极点和零点均位于s左半平面，则系统称为最小相位系统。如果系统至少有一个极点或零点位于s右半平面，则系统称为非最小相位系统。对于非最小相位系统之根迹绘制，要注意其幅角条件的变化。

例4-7 状态空间模型的概念说明

设一非最小相位系统如图4-22所示，试作出其根迹。

图4-22

⑴.常规方法

本系统的幅角条件为：

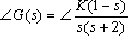
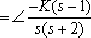
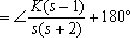
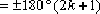
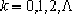
即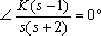

据上面方程可以作出如图4-23所示
根轨迹。

⑵.“MATLAB”方法

解本题的MATLAB程序exe47.m：

n=[-1 1];
d=[1 2 0];
rlocus(n,d)
title(‘4-23’)

执行本程序,可得非最小相位系统根轨迹，如图4-23所示。

图4-23

⑶.附言：

从这个系统的根轨迹图，可以看出当根增益 小于2时，系统是稳定的。