频率响应法-- 频域性能指标和时域性能指标的关系
频率响应法-- 频域性能指标和时域性能指标的关系
频域性能指标和时域性能指标的关系
频率响应法是通过系统的开环频率特性和闭环频率特性的一些特征量间接地表征系统瞬态响应的性能,因而这些特征量又被称为频域性能指标。常用的频域性能指标包括:开环频率特中的相位裕量、增益裕量;闭环频率特中的谐振峰值、频带宽度和谐振频率等。在时域分析中,控制系统包括静态性能指标和动态性能指标。虽然这些频域性能指标没有时域性能指标那样直观,但对于二阶系统而言,它们与时域性能指标间有着确定的对应关系;在高阶系统中,只要存在一对闭环主导极点,则它们也有着近似的对应关系。 5.6.1 开环频率特性中相位裕量与时域性能指标的关系 关于开环频率特性低频段与闭环系统静态性能的关系我们在5.3.4中已作了分析,此处我们着重研究二阶系统的相位裕量 当 |
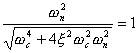 |
求解上式,得
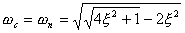 | |
| (5-60) |
据此求得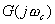 的相角为
的相角为
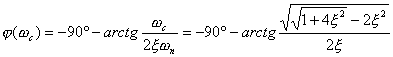 | |
| (5-61) |
由相位裕量的定义得
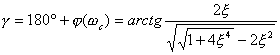 | |
| (5-62) |
图5-59为 与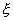 的关系曲线。
的关系曲线。
1、 与超调量的关系
在前面第三章已知,超调量 和阻尼比 之间的定量关系为
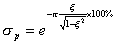 | |
| (5-63) |
将式(5-62)和式(5-63)的函数关系,以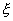 为横坐标,
为横坐标,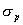 和
和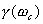 为纵坐标,绘制于同一张图上,如图5-60所示。这样,根据给定的相位裕量
为纵坐标,绘制于同一张图上,如图5-60所示。这样,根据给定的相位裕量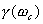 就可由图5-60直接得到时域特性的最大超调量
就可由图5-60直接得到时域特性的最大超调量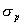 。反之,当要求超调量不超过某一允许的
。反之,当要求超调量不超过某一允许的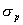 值时,也可以从图5-60中求得应有的相信裕量
值时,也可以从图5-60中求得应有的相信裕量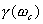 。
。
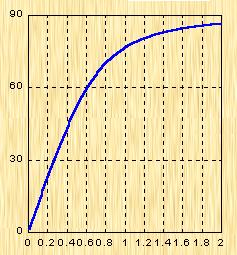 |
| 图5-59 二阶系统的相位裕量与阻尼比关系 |
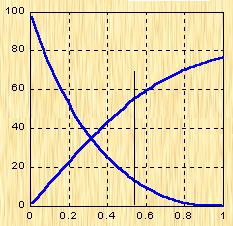 |
| 图5-60 二阶系统相位裕量、最大超调量与阻尼比关系 |
2、 与调整时间的关系
相位裕量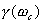 与调整时间
与调整时间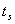 之间的定量关系。仍以二阶系统为例,在第三章已求得调整时间
之间的定量关系。仍以二阶系统为例,在第三章已求得调整时间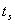 的近似表达式
的近似表达式
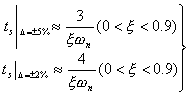 | |
| (5-64) |
将式(5-60)代入式(5-64)可得
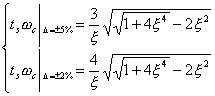 | |
| (5-65) |
再由式(5-62)和式(5-65)可得
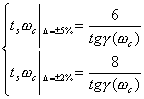 | |
| (5-66) |
将式(5-66)的函数关系绘成曲线,如图5-61所示(图中画的是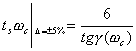 的关系式)。
的关系式)。
如果有两个系统,其相位裕量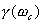 相同,那么他们的最大超调量
相同,那么他们的最大超调量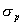 (时域)是大致相同的,但他们的调整时间
(时域)是大致相同的,但他们的调整时间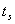 并不一定相同。由式(5-66)可知,
并不一定相同。由式(5-66)可知,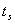 与剪切频率
与剪切频率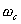 成反比,即
成反比,即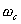 越大,时域的调整时间
越大,时域的调整时间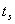 越短。所以剪切频率
越短。所以剪切频率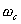 在频率特性中是一个很特殊的重要参数,它不仅影响系统的相位裕量,还影响动态过程的调整时间
在频率特性中是一个很特殊的重要参数,它不仅影响系统的相位裕量,还影响动态过程的调整时间
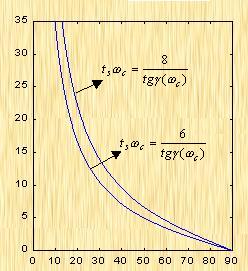 |
| 图5-61 |
上述的频域性能与时域性能的定量关系都是基于二阶系统得出来的。对于高阶系统,只要存在一对闭环主导极点,就可以利用上述二阶系统分析的一些定量关系,以简化系统的设计
5.6.2 闭环频率特性及其特征量
由于开环和闭环频率特性间有着确定的关系,因而可以通过开环频率特性求取系统的闭环频率特性。对于单位反馈系统,其闭环传递函数为
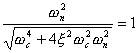 |
对应的闭环频率特性为
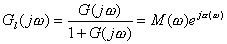 | |
| (5-67) |
上式描述了开环频率特性与闭环频率特性之间的关系。如果已知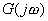 曲线上的一点,就可由式(5-67)确定闭环频率特性曲线上相应的一点。
曲线上的一点,就可由式(5-67)确定闭环频率特性曲线上相应的一点。
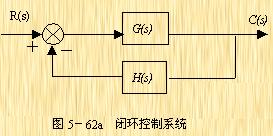
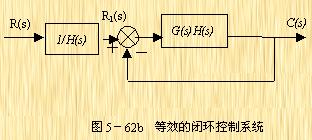
对于非单位反馈系统,如图5-62a,则可先将其等效为如图5-62b的系统,然后按上法先求图5-62b中单位反馈系统的频率特性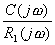 ,再与频率特性
,再与频率特性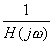 相乘,即可得到总的闭环频率特性。
相乘,即可得到总的闭环频率特性。
 |
 |
用这种方法逐点绘制闭环频率特性曲线,在工程上,常用等M圆、等N圆和Nicoles图线来表示闭环系统的频率特性,并用用图解法去绘制。显然这是既繁琐又费时间的工作。现在这些工作可由计算机软件实现,例如在Matlab中就有专门的绘制等M圆、等N圆和Nicoles图线的函数,从而大大提高了绘图的效率和精度。本节我们不对闭环频率特性的绘制方法进行研究,仅对闭环频率特性与时间性能指标间的关系作些分析。
1. 闭环频率特性的谐振峰值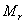 与谐振频率
与谐振频率
在本章第三节,针对二阶系统我们给出了二阶振荡环节的谐振峰值 和谐振频率 的概念,闭环系统的幅值在谐振频率 处所取得的最大值 ,称为谐振峰值。如图5-63所示。
2. 截止频率和频带宽度
图5-63为 时闭环对数幅频特性的一般形状。当幅频值下降到低于零频率值以下3dB时,对应的频率 称为截止频率,即有
对应于闭环幅频值不低于-3dB的频率范围 ,通常称为系统的频带宽度。系统的频带宽度反映了系统复现输入信号的能力,具有宽的带宽的系统,其瞬态响应的速度快,调整的时间也小。
| 图5-63 闭环频率特性的性能指标 |
例5-11 试比较两个系统带宽的大小,并验证...
设有二个控制系统,它们的传递函数分别为
系统I:
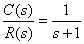 |
系统Ⅱ:
试比较两个系统带宽的大小,并验证具有较大带宽的系统比具有较小带宽的系统响应速度快,对输入信号的跟随性能好。
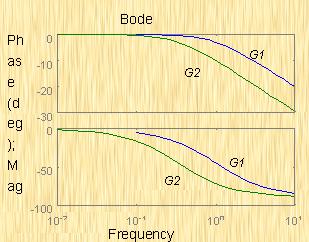 |
| 图5-64a 两系统的闭环对数幅频特性 |
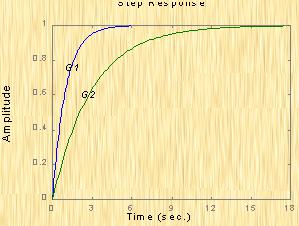 |
| 图5-64b 两系统的单位阶跃响应曲线 |
解 图5-64a为上述两系统的闭环对数幅频特性曲线(图中虚线为其渐近线)。由图可见,系统I的带宽为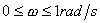 ,系统Ⅱ的带宽为 ,即系统I的带宽是系统Ⅱ带宽的三倍。图5-64b表示了两系统的阶跃响应曲线。显然,系统I较系统Ⅱ具有较快的阶跃响应,并且前者跟踪阶跃输入的性能也明显优于后者。
,系统Ⅱ的带宽为 ,即系统I的带宽是系统Ⅱ带宽的三倍。图5-64b表示了两系统的阶跃响应曲线。显然,系统I较系统Ⅱ具有较快的阶跃响应,并且前者跟踪阶跃输入的性能也明显优于后者。
需要指出,宽的带宽虽然能提高系统响应的速度,但也不能过大,否则会降低系统过滤高频噪声的能力。因此在设计系统时,对于频带宽度的确定必须兼顾系统的响应速度和抗高频干扰的要求,采取一种折衷的方案。
5.6.3 闭环频域特性与时域响应性能指标的关系
对于二阶系统,其时域响应与频域响应之间有着确定的对应关系。标准二阶系统对应的闭环频率特性为
| (5-68) |
式中
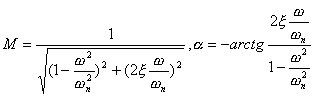 |
当 时,系统有谐振产生,由本章第三节讨论可知,其谐振峰值分别为
| (5-69) |
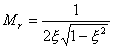 | |
| (5-70) |
由式(5-70)得
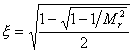 | |
| (5-71) |
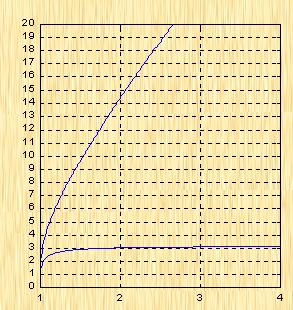
1、谐振峰值 和最大超调量 的关系
为了便于对谐振峰值 和最大超调量 作比较,把 和 与 的关系曲线都画在图5-65中。由图可见, 和 均随着 的减小而增大。显然,对于同一个系统,若在时域内的 大,则在频域中的 必然也是大的;反之亦然。为了使系统具有良好的相对稳定性,在设计系统时,通常取 值在 之间,对应的 将坐落在 之间。
把式(5-70)代入式(5-63),则得
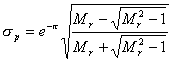 | |
| (5-72) |
如果已知 ,则由上式可求得对应的 。
| 图5-65 谐振峰值 和最大超调量 的关系 |
 |
| 图5-66 和 , 关系 |
2、谐振峰值 和调整时间 、峰值时间 关系
根据在第三章中导出二阶系统的上升时间和调整时间的关系式,并考虑到式(5-69),则得
| (5-73) |
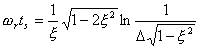 | |
| (5-74) |
由式(5-70)有:
 | |
| (5-75) |
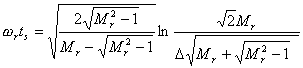 | |
| (5-76) |
将式(5-75)的函数关系用曲线表示,如图5-66。可见,峰值时间 与谐振峰值
与谐振峰值 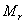 成正比,而峰值时间
成正比,而峰值时间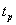 与谐振频率 成反比。调整时间 与 和 的关系和峰值时间 与它们的关系相同。同时上述两式表明,如果已知 和 ,就能从上述关系式中求出 和 。
与谐振频率 成反比。调整时间 与 和 的关系和峰值时间 与它们的关系相同。同时上述两式表明,如果已知 和 ,就能从上述关系式中求出 和 。
3、频带宽度与峰值时间、调整时间的关系
根据频带宽度的定义,当 时,二阶系统的幅频为
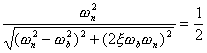 |
求解上式,得
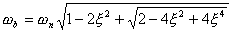 | |
| (5-77) |
同理,注意到式(5-73)、(5-74),并对照式(5-69),则得
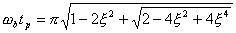 | |
| (5-78) |
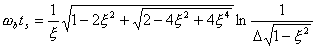 | |
| (5-79) |
由式(5-78)和(5-79)可知,对于给定的 , 和均与 成反比。这就是说, 越大,则系统响应的速度就越快。
把式(5-70)代入式(5-78)、(5-79),可求得
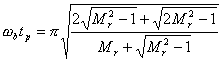 | |
| (5-80) |
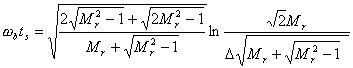 | |
| (5-81) |
上述两式把时域性能指标 、 与频域性能指标 和 联系起来,如果已知 和 ,就能从上述关系式中求出 和 。
对于高阶系统,系统的频率响应与时域响应间的对应关系可通过经验公式联系,也通过傅氏积分,即,
| (5-82) |
由于这种积分变换较复杂,因而不可能像二阶系统那样简单地描述频域响应与时域响应间的对应关系,其积分一般借助于计算机辅助算法,且目前这些算法均比较成熟。如果高阶系统中有一对共轭主导极点,则上述二阶系统的时域响应与频域响应间的对应关系就可近似地应用于高阶系统中去。



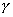 、剪切频率
、剪切频率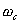 与阻尼比
与阻尼比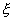 间的关系。
间的关系。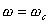 时,
时,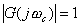 ,即
,即
评论