RC低通滤波器和RC高通滤波器的工作原理
RC低通滤波器
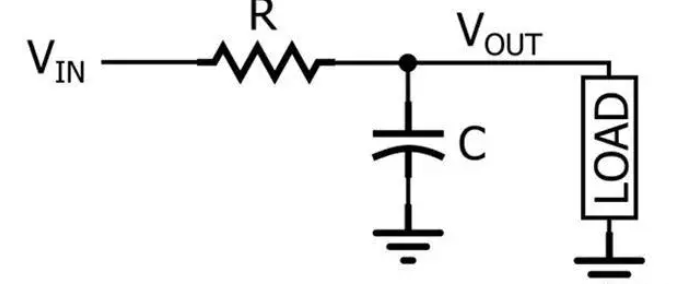
理解低通滤波器其实很简单,在一个频率下把电容看作是一个电阻,那把R和C就看作是串联,那么VOUT就是分压点。
我们想要滤掉某个频率,就让电容在这个频率容抗很小,分压就会很小。如果比这个频率高,那么根据容抗公式可知,容抗会越小,分得的电压就越小,同理频率越低分得的电压就越高,也就是频率低的可以更多的通过,频率高通过的量少,所以该电路叫低通滤波器。
我们在书本上可以知道该电路有一个截止频率f=1/2πRC,通过这个截止频率就可以计算得到一个合适的RC组合。那么这个公式怎么来的呢?其实是通过传递函数得到幅频特性然后推出来。上图的传递函数为:
G(S)=1/(RCS+1)
从而得到它的幅频特性为:
A(ω)=1/(RCωj+1)
他的模为:
| A(ω)|=1/√([RCω]^2+1)
我们知道截止频率是指在幅度被衰减3dB时的频率点,也就0.707倍:
1/√([RCω]^2+1)=1/√2
所以
[RCω]^2+1=2
化简得
ω=1/RC
ω=2πf,那么截止频率的公式不就出来了。
我们在设计这种电路的时候,我们是知道截止频率的,直接上的公式来套,发现并不能滤得很好,那是因为这个频率时针对正弦波也就是针对基波进行叙述的,如果是滤除方波或者其他波上的干扰信号记得保留有用信号的主要谐波成分,要不然有用信号都会被滤掉。所以我们在给方波信号滤除噪声时,截止频率点要取方波频率的3-5倍。
取得f这个频率点的RC组合很多,但是并不是每种组合都是对的,这里涉及到了阻抗匹配的问题,要尽量满足RC的阻抗大于信号源发内阻,要远小于负载阻抗,这样才能保证信号衰减少一些。
RC高通滤波器
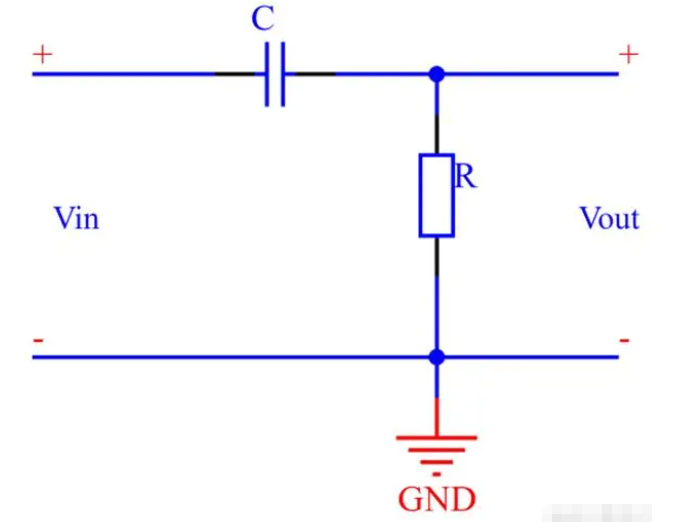
通过电路结构就可以发现,它与低通滤波器是反的,考虑的点从电容变成了电阻。工作原理还是可以按串联反压的方式去理解。
相比低通滤波器结构变了,传递函数也变量,但是我们在书本上看到高通的截止频率还是f=1/2πRC,这个是为什么呢?接下来我们推导一下就知道了。
它的传递函数为:
G(S)=1/(1/RCS+1)
它的幅频特性为:
A(ω)=1/(1/RCωj+1)
它的模为:
| A(ω)|=1/√(1/[RCω]^2 +1)
幅度被衰3dB,得:
1/√([RCω]^2+1)=1/√2
所以
[RCω]^2+1=2
则
ω=1/RC
可以发现他确实跟低通滤波器的截止频率一样,所以我们在设计电路,学习电路不要像背诵口诀一样,我们要知其所以然。



评论